100 - Bits
Approach #1
Try to swap each pair of bits once, and choose the maximum value. Complexity: O(log2 N)
Approach #2
The maximum value can be obtained by swapping the first occurrence of a 0 bit with the last occurrence of a 1 bit. Complexity: O(log N).
Haskell implementation:
import Numeric (showIntAtBase, readInt) import Data.Char (intToDigit, digitToInt) import Data.List bin x = showIntAtBase 2 intToDigit x "" dec s = foldl' (\acc x -> acc * 2 + digitToInt x) 0 s best x | not (elem '0' x) = x | not (elem '1' x) = x | firstZero > lastOne = x | otherwise = front ++ "1" ++ middle ++ "0" ++ back where front = take firstZero x middle = take (lastOne-firstZero-1) (drop (firstZero+1) x) back = drop (lastOne+1) x firstZero = head $ elemIndices '0' x lastOne = last $ elemIndices '1' x main = do input <- getContents let xs = map read $ words $ last $ lines input :: [Int] putStrLn $ concat $ intersperse " " $ map (show . dec . best . bin) xs
250 - Compress
Approach #1
For one component, the range of hexadecimal values is [0, 255] (that is, from #00 to #FF). Moreover, there are only 16 candidates (compressible values): #00, #11, …, #FF.
The actual pixel component can be converted to base 10. All 16 candidates can be converted to base 10 as well: they all belong to the set {x*16+x | 0 ≤ x ≤ 15}. At this point, we choose the candidate which has the smallest absolute difference compared to the original value.
Haskell implementation:
import Numeric import Data.Char (toUpper) data Pixel = Pixel Int Int Int deriving (Eq, Show) pixelFromList (r:g:b:_) = Pixel r g b pixelFromList _ = error "Pixel must have 3 components" hexToDec = fst . head . readHex decToHex x = map toUpper $ showHex x "" compressP (Pixel r g b) = pixelFromList $ map compress [r,g,b] compress n = snd $ minimum $ map (\x -> (abs (x-n), x)) compressibles where compressibles = [x*16+x | x <- [0..15]] showCompressedP (Pixel r g b) = '#' : (foldr (:) [] $ map (last . decToHex) [r,g,b]) readP s = pixelFromList $ map hexToDec [r, g, b] where r = take 2 $ tail s g = take 2 $ drop 3 s b = drop 5 s main = do input <- getContents let image = map (map (showCompressedP . compressP . readP) . words) $ drop 1 $ lines input sequence $ map (putStrLn . unwords) image
Approach #2
Upon closer inspection, we notice that the set of candidates can be reduced to just a select few. Consider the component #XY (where X and Y are hexadecimal digits). The most natural decision is to only change Y to match X, leading to the compressible value #XX. This works well in cases such as #14 → #11 (delta = 3), but performs sub-optimally in other scenarios: #1F → #22 (delta = 2) is a better choice than #1F → #11 (delta = 14).
The optimal decision in such cases is to only change X by one unit, leading to the compressible #(X-1)(X-1) or #(X+1)(X+1). We choose whichever value is closest to #XY.
Python implementation:
#!/usr/bin/python3 import sys def diff(x, y): return abs(int(x, 16) - int(y, 16)) def compress(x): a = max('0', '9' if x[0] == 'A' else chr(ord(x[0])-1)) b = x[0] c = min('F', 'A' if x[0] == '9' else chr(ord(x[0])+1)) return min([(diff(a+a, x), a), (diff(b+b, x), b), (diff(c+c, x), c)])[1] def compressPixel(p): return "#%c%c%c" % (compress(p[1:3]), compress(p[3:5]), compress(p[5:])) def main(): n, m = map(int, input().split()) for line in sys.stdin: print(' '.join(list(map(compressPixel, line.split())))) if __name__ == '__main__': main()
750 - Buckets
Because two subsequences will be in the same bucket if they have the same elements, their position does not really matter.
Let's fix a some arbitrary frequencies for all the elements in our initial array.
Let this array be a
a[i]= the arbitrary frequency of the number i
Let's also denote:
freq[i] = the total frequency of the number i in the whole array
Note that a[i] ≤ freq[i] for each i
The size of the bucket containing all these subsequences with be: 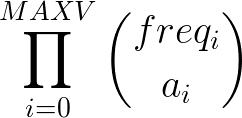
Now we only need a way to compute the sum of products of all possible a. We can compute the product of a sum which will give us every single possbile combination. This product is the following: 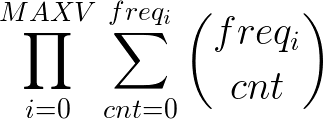
In the end, because we want the size of each bucket to be squared, and remove the empty set, we need to compute the following formula: 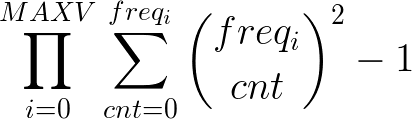
800 - Gas Stations
It can be observed that the queries can be divided in two categories. Those smaller than sqrt(n)(square root of n) and those bigger.
For the queries bigger than sqrt(n) the solution is simple. Go through the segments of 0's with length > sqrt(n) and calculate how many gas stations have to be built. The formula is length / capacity for full segments between A and B and almost identical for the suffix after A and prefix before B. The complexity for a query is O(sqrt(n)) because you can't have more segments of this type.
For queries smaller than sqrt(n) the formula is the same, but we have too many segments, so we have to do preprocessing to answer fast.
We can build an array L where L[i] = the length of i'th segment of 0's and Sum where Sum[i][j] = sum(L[x] / j) with x <= i and j <= sqrt(n). The preprocessing takes O(n*sqrt(n)). After these computations, we can see that for a query we need the range of full segments of 0's between A and B, this is also a simple precomputation. The query can be now answered in O(1) .
!Also the memory can be optimised from O(n*sqrt(n)) to O(n) by sorting the queries increasingly by capacity. But this wasn't a requirement for full score.


