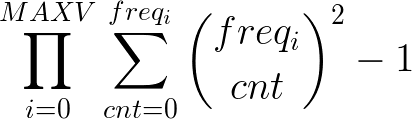King of Buckets is very nervous lately. His treasure keepers have found a new way to keep track of how much gold he has that does not allow any eavesdropper to know the exact size of the treasure. Now all he can see every month is a number which he doesn't know how to interpret. What if they are secretly stealing his gold!?
The treasure looks like this: there are N boxes, each of them labeled with an integer L, depending on the contents of the box. They have been arranged over time in a straight line, in the order in which the king had received them from admirers. To compute the value of the treasure, the treasure keepers take each non-empty subsequence of boxes and assign it to a bucket. Different subsequences will be assigned to the same bucket if they contain the same labels, regardless of the order. The value of the treasure is computed as SUM(|bucket(i)|2), where |bucket(i)| represents the number of subsequences assigned to the ith bucket, for 1 ≤ i ≤ the number of resulting buckets.
For instance, if the treasure is formed from 1, 2, 2, 3, 1 (i.e. one box with label 1, two consecutive boxes with label 2 and so on) then {1, 2, 3}, {1, 2, 3}, {2, 3, 1} and {2, 3, 1} are all part of the same bucket, whereas {3} is alone in its bucket. Note that {1, 2, 3} and {1, 2, 3} are different subsequences because in the first case 2 is taken from the 2nd position in the string, whereas in the second case it is taken from the 3rd position.
Note: A subsequence of an array S = s1, s2, …, sn is an array S' = si1, si2, …, sik such that 1 ≤ i1 < i2 < … < ik ≤ n, and k ≥ 1.
Input
On the first line there will be the number N of boxes in the treasure, followed on the next line by N integer numbers representing the labels.
Output
The value S of the treasure, as computed by the treasure keepers.
As this number can be very large, please print the number modulo 109 + 7
Restrictions
- 1 ≤ N ≤ 105
- 1 ≤ L ≤ 106
Sample
| Input | Output | Explanation |
|---|---|---|
| 3 1 2 2 | 11 | The subsequences of labels are: {1}, {2}, {2}, {1, 2}, {1, 2}, {2, 2} and {1, 2, 2}. The following buckets are created: SUM(|buckets(i)|2) = 12 + 22 + 22 + 12 + 12 = 11 |
| 5 1 2 2 3 1 | 71 | This one is a bit tricky. |
Because two subsequences will be in the same bucket if they have the same elements, their position does not really matter.
Let's fix a some arbitrary frequencies for all the elements in our initial array.
Let this array be a
a[i]= the arbitrary frequency of the number i
Let's also denote:
freq[i] = the total frequency of the number i in the whole array
Note that a[i] ≤ freq[i] for each i
The size of the bucket containing all these subsequences with be: 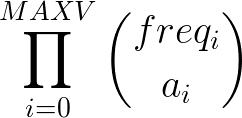
Now we only need a way to compute the sum of products of all possible a. We can compute the product of a sum which will give us every single possbile combination. This product is the following: 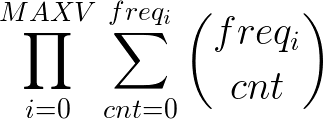
In the end, because we want the size of each bucket to be squared, and remove the empty set, we need to compute the following formula: