As you may know, even recycled problems have their place in programming competitions. This is one such problem.
Let us recall the definitions from Peculiar Function: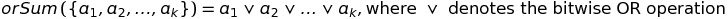
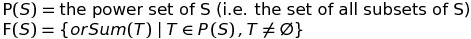
You are given an integer K. Your task is to find a set S such that F(S) contains exactly K elements.
Input
An integer K.
Output
The first line of output should contain the number of elements in the set S.
The second line of output should contain the elements of S separated by spaces, in any order.
Constraints
- 1 ≤ K ≤ 1000
- 1 ≤ any value of S ≤ 5000
Sample
| Input | Output | Explanation |
|---|---|---|
| 3 | 2 3 4 | F({3, 4}) contains the following values:
|
Approach #1 (Costin Andrei Oncescu)
Let y = 2i be the smallest power of 2 strictly greater than K. We choose as the elements of S all values in the interval [y-k, y-1].
Consequences:
- We already have exactly K values in S. Each value will constitute a subset by itself, and provide a distinct value in F(S).
- For any two values a, b ∈ [y-k, y-1], we have (a OR b) ∈ [y-k, y-1]. In other words, there will be no additional values generated by larger subsets of S. To better understand the intuition behind this, try to imagine the binary representation of all values in the given interval.
Approach #2 (Sergiu Puscas)
Since the constraints for this problem are not very strict, we can try to construct a solution in the following way:
- Start with S = {1} (or any other value).
- While |F(S)| ≠ K:
- If |F(S)| < K, choose a new value randomly and add it to the set.
- If |F(S)| > K, choose an existing value randomly and remove it from the set.
- Print the elements of S.
This approach finds a solution relatively quickly, assuming an efficient implementation of the method that computes F(S).
In practice, it yields a set that is much smaller than than K elements.


