A pharmer owns a rectangular pharm sized n×m. In order to break from the mundane, he devised a plan for his 2015 seasonal crops. He drew a map of his pharm, and colored each unit cell according to which type of crop he was going to cultivate on it. The same crop type can be grown on multiple cells.
As a consequence, different color zones can be spotted on his map. Two cells belong to the same zone if they share a common edge, and have the same color. The pharmer decided to only provide water to a single zone (the largest one), so he's now wondering which zone to choose. Moreover, he is willing to change the crop on a single unit cell, if that meant he would obtain a new largest zone. Your task is to help him achieve his goal.
Input
The first line of input contains an integer type, 1 ≤ type ≤ 2.
The second line of input contains integers m and n.
Each of the following m lines contains a sequence of n lowercase letters, indicating the color codes of the crop cultivated on each cell.
Output
If type = 1, you should only output one integer, equal to the maximum surface of any zone on the pharmer's map.
If type = 2, you should output the following:
- on the first line, two integers x and y, indicating the coordinates of the cell which can be replanted in order to obtain a new largest zone.
- on the second line, a single lowercase letter, indicating the color code of the new crop which should be planted at coordinates (x, y).
Constraints
- 2 ≤ m ≤ 400
- 2 ≤ n ≤ 400
- 2 ≤ the total number of different crops ≤ 26
- 30% of all testcases will ask the first type of question.
- 70% of all testcases will ask the second type of question.
- For the second question, in case of multiple cells that grant the same maximum sized zone, you should output the first one, lexicographically.
- Each test will be scored separately. Your final score will be equal to the sum of all tests' scores.
- This statement was written by Phteven.
Sample
| Input | Output |
|---|---|
| 1 7 8 rmmgggaa mvvgggaa mvvgvvvv vvvrvvvv vvrrrgga vvrrrggg aaaaaaag | 11 |
| 2 7 8 rmmgggaa mvvgggaa mvvgvvvv vvvrvvvv vvrrrgga vvrrrggg aaaaaaag | 3 4 v |
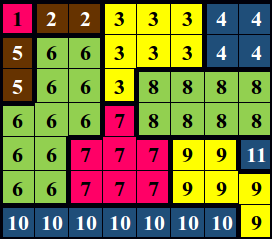 | First case: the largest zone is #6. It contains 11 cells. Second case: by coloring the (3, 4) cell green, zones #6 and #8 would become a single zone (surface = 20). |
The easy solution (Marius Gavrilescu)
We will use a flood fill function that computes the area of a zone.For the first kind of queries we will call the function for each cell and print the largest value returned by the function.
For the second kind of queries, if we change the color of a cell, we should change it to the color of one of its neighbours (otherwise it does not increase the area of a region). Thus, for each cell we can take each of its neighours, change the color of the cell to that of the neighbour and call our fill function.
1 #include<stdio.h> 2 const int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1}; 3 4 char v[405][405]; 5 int us[405][405], filln = 1; 6 7 int fill(int x, int y, int c){ 8 int ans = 1; 9 us[x][y] = filln; 10 for(int i = 0; i < 4; i++){ 11 int nx = x + dx[i], ny = y + dy[i]; 12 if(v[nx][ny] == c && us[nx][ny] < filln) 13 ans += fill(nx, ny, c); 14 } 15 return ans; 16 } 17 18 int main(void){ 19 int t, m, n; 20 scanf("%d%d%d ", &t, &m, &n); 21 for(int i = 1; i <= m; i++) 22 scanf("%s ", &v[i][1]); 23 24 int best = 0, bestx, besty, cur; 25 char bestc; 26 for(int x = 1; x <= m; x++) 27 for(int y = 1; y <= n; y++){ 28 cur = fill(x, y, v[x][y]); 29 if(cur > best) 30 best = cur, bestx = x, besty = y, bestc = v[x][y]; 31 if(t == 1) 32 continue; 33 for(int k = 0; k < 4; k++){ 34 int nx = x + dx[k], ny = y + dy[k]; 35 if(!v[nx][ny] || v[nx][ny] == v[x][y]) 36 continue; 37 cur = fill(x, y, v[nx][ny]); 38 filln++; 39 if(cur > best) 40 best = cur, bestx = x, besty = y, bestc = v[nx][ny]; 41 } 42 } 43 44 if(t == 1) 45 printf("%d\n", best); 46 else 47 printf("%d %d\n%c\n", bestx, besty, bestc); 48 return 0; 49 }
The fast solution (Gabriel Inelus)
A more efficient way of solving the type 2 queries is the following:First of all we should define some helping structures:
- Let a component be the maximal region of the same colour. A position (x,y) is a member of the component C if and only if Fill(x,y) denotes the full component C.
- Let quant be an array which contains the area of a specific component.
- Let used mean both that the coordinate (x,y) has been visited and also used[x][y] means to which component does (x,y) belong.
Then, we can use these structures as follows: quant[used[x][y]] is the area of the component that (x,y) belongs to.
To answer the type 2 query, we must scan the matrix and for each (x,y) we should test the relevant characters (only the ones of the 4 neighbours) and use the quant vector to calculate the new area.
The complexity of this algorithm is O(N*M*K) where K = 16 (for every position we choose 4 neighbours and 4 colours)


