A Fibonacci tree is defined in the following way: on level 0 there is the root, which has a single child on level 1. Then each node from level i, with i > 2, has as many children as its parent together with its grandparent (its parent's parent).
Then we do a breadth first search traversal of the tree and we label all the nodes with numbers starting from 1 and increasing with 1 unit, beginning with the root.
Each node is initially inactive and it will be activated once an operation of type 1 is performed on it. More generally, the operations we can choose to perform on the tree are as follows:
- 1 X Y Z - increase with Z the value assigned to the least common ancestor of the nodes labeled by X and Y. Note that Z can be negative, which means you are actually decreasing the value. Also, if the value from that node is empty, then you should consider it as being 0 before adding.
- 2 X Y - compute the maximum value assigned to a node from the closed interval [X, Y]. However, be aware that you should not consider the yet inactive nodes (so here, if a node is inactive, don't suppose its value is 0, simply ignore that node). Note that it is possible for all the nodes to be inactive. In that case, print "Comisia" instead.
Input
The first line of input contains a single integer M - the number of operations.
The next M line of input contains one of the described operations, having the format above.
Output
For each operation of type 2, print the requested value.
Restrictions
- 1 ≤ M ≤ 105
- 1 ≤ X ≤ Y ≤ 1018
- -1012 ≤ Z ≤ 1012
Sample
| Input | Output | Explanations |
|---|---|---|
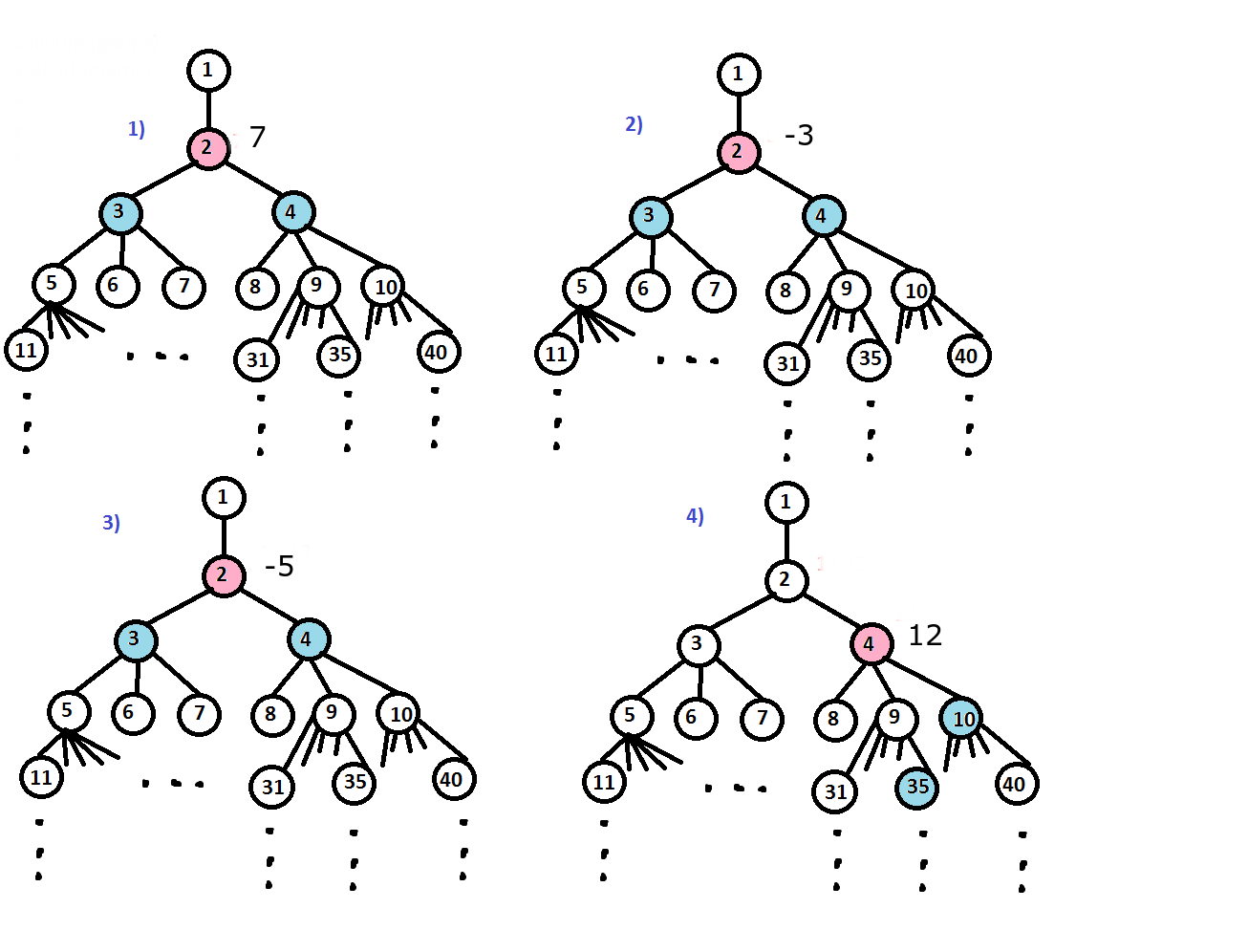
| 7 1 3 4 7 2 3 4 1 3 4 -10 1 3 4 -2 1 10 35 12 2 1 10000 2 1 3 | Comisia 12 -5 | The values from each node are described in the picture below. For the first query, the interval is [3, 4]. Both 3 and 4 are empty-valued, as only 2 has a non-void value (7), so we print "Comisia" For the second query, the interval is [1, 10000]. The only non-empty nodes are 2 (-5) and 4(12). So the maximum among all of them is 12. For the third query, the interval is [1, 3]. The only non-empty nodes are still 2(-5) and 4(12). So the maximum among the ones that are in the closed interval [1, 3] is -5. |