Consider the following: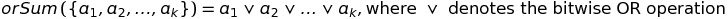
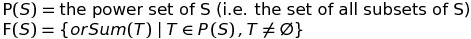
Given a set S1 of positive integers, compute the minimum size of a set S2 (possibly equal to S1) so that F(S1) = F(S2).
Input
The first line of input contains the size of S1.
The second line of input contains the elements of S1, separated by spaces.
Output
A single integer: the minimum size of S2.
Constraints
- 1 ≤ the size of S1 < 219
- 1 ≤ every element of S1 < 219
Notes
- If you use C++ I/O streams, please add
cin.sync_with_stdio(false);before reading the input, in order to improve I/O speed. - The elements of a set are distinct, by definition.
Sample
| Input | Output | Explanation |
|---|---|---|
| 4 5 10 15 25 | 3 | S1 = {5, 10, 15, 25} F(S1) = {5, 10, 15, 25, 27, 29, 31} S2 = {5, 10, 25} F(S2) = {5, 10, 15, 25, 27, 29, 31} |
The first observation we can make is that 0 ≤ orSum(S') < 2^19 for any subset S' of S1. Let's see if we can construct a set Q, having 0 ≤ orSum(Q) < 2^19 using the integer values from S1. It is enough to consider for this all elements of S1 which are completely included in Q. An element x is completely included in a set S if orSum(S) | x = orSum(S), i.e. there is no position 0 ≤ i < 19 for which orSum(S) & 2^i == 0 and x & 2^i != 0. If these are not enough to form Q, then we cannot obtain Q at all.
We now need to compute for each such Q the orSum of all elements “completely included†in S1. We can compute dp[x] = orSum(dp[x - 2^i]), where 0 ≤ i < 19 and x & 2^i == 2^i. Remark: if x belongs to S1, then dp[x] = x.
Now, S2 needs to contain all numbers x having dp[x] = x and orSum({dp[x - 2^i] where 0 ≤ i < 19 and x & 2^i == 2^i}) < x. This assures us that they cannot be generated by applying orSum on a subset of numbers from S1, so they must be in S2.


