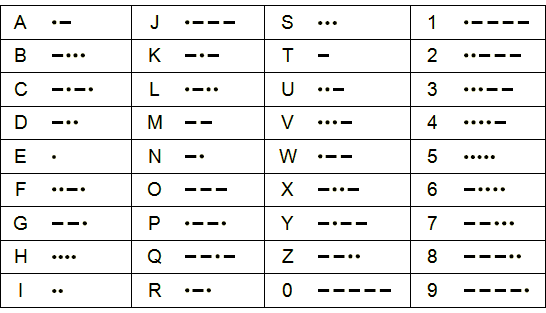
Morse code is a method of transmitting text information as a series of on-off tones, lights, or clicks that can be directly understood by a skilled listener or observer without special equipment. It works by mapping each letter of the English alphabet to a sequence of up to 4 characters, either dashes or dots.
Because of the non-constant sequence sizes, different letter encodings must be separated in order to prevent ambiguity.
For instance, the sequence —•—••— may have different interpretations, depending on how one chooses to separate the symbols:
Two words are called similar if they have the same Morse representation, without symbol separation. In the example above, ca, nna, cet and nnet are all similar to each other.
You are given a set containing N different words. Your task is to find the largest subset such that any two words in the subset are similar.
Input
The first 26 lines of input contain each letter of the alphabet, along with its Morse encoding.
The next line contains N. Each of the following N lines contains a word.
Output
A single integer: the size of the largest subset in which any two words are similar to each other.
If there are no similar words, the answer is -1.
Constraints
- Sum of all word lengths ≤ 105
- All words contain only lowercase English letters.
Sample
| Input | Output | Explanation |
|---|---|---|
| a .- b -... c -.-. d -.. e . f ..-. g --. h .... i .. j .--- k -.- l .-.. m -- n -. o --- p .--. q --.- r .-. s ... t - u ..- v ...- w .-- x -..- y -.-- z --.. 5 ca nna abc nnet cat | 3 | Words ca, nna and nnet are all represented in Morse as —.—..—. They form the largest subset with the required property. Words abc (•——•••—•—•) and cat (—•—••——) have unique representations. |
Let's say we are at word W(i). We compute its morse encoding and using a mapping from morseEncoding to number of apparitions, we will keep track of how many times a morse encoding appeared in the dictionary.
So at step i we will increment the number of apparitions of the morse encoding we obtained from W(i) where i=1...n. In order the manage this mapping we can use a hash table that maps strings to integers. We can then compute the answer by iterating through the values of the hash.
If there are no collisions, we print -1.
#include <iostream> #include <stdio.h> #include <unordered_map> #include <vector> using namespace std; int main() { int n, ans = 0; vector <string> d; unordered_map<char, string> repr; unordered_map<string, int> cnt; for(int i = 0; i < 26; ++ i) { char ch; string code; cin >> ch >> code; repr[ch] = code; } cin >> n; for(int i = 0; i < n; ++ i) { string word; cin >> word; string morse = ""; for(auto ch : word) morse = morse + repr[ch]; ans = max(ans, ++ cnt[morse]); } if(ans == 1) cout << -1 << '\n'; else cout << ans << '\n'; return 0; }


