Mesh

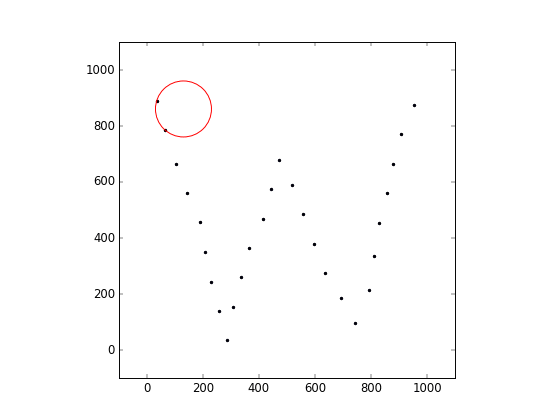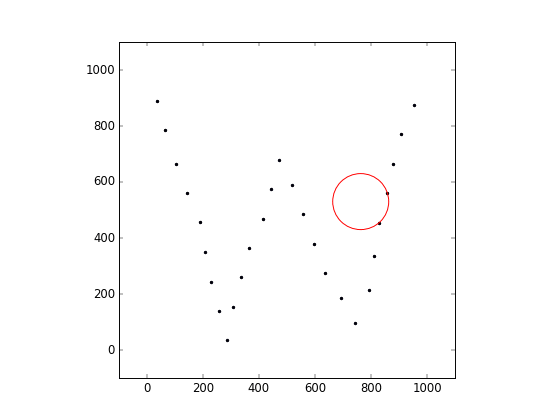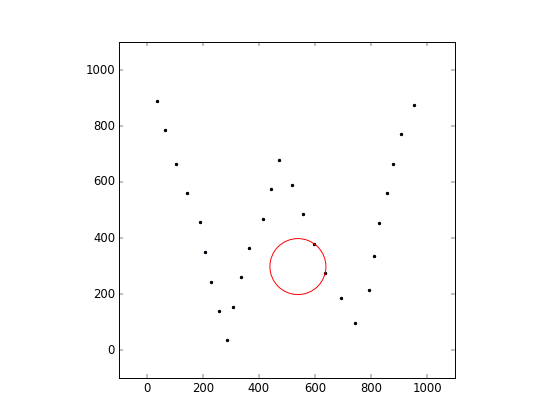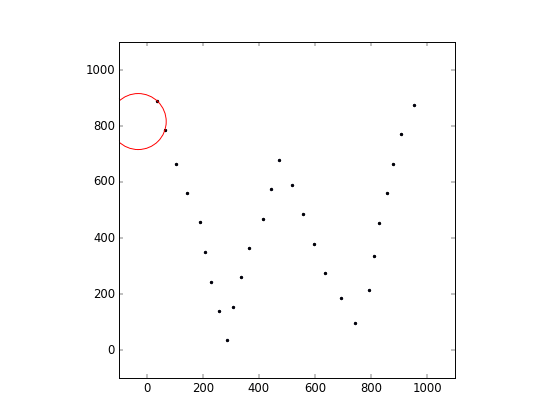
Consider a set of N points with floating point coordinates (x_i, y_i), 1 ≤ i ≤ N in the two-dimensional space, and a circle of radius R.

The circle is initially placed at coordinates (Cx, Cy), and touches two points with indices a, b (that is, the two points are on the surface of the circle, and there are no points inside). An operation is defined by choosing one of the two points on the circle and using it as a pivot. The circle is rotated smoothly around the pivot, until it touches some other point. During an operation, the circle must be in contact with the pivot, and no points can lie inside of it.

Operations can be applied in any order, and points can be reached multiple times. Your task is to determine the largest possible set of points that can be reached by the circle, after any number of operations.

Input

The first line of input contains integers N, R.
The second line of input contains integers a, b.
The third line of input contains two real values: Cx, Cy.
Each of the following N lines contains two real values x_i, y_i.

Output

The first line of output should contain K - the size of the largest set of reachable points.
The second line of output should contain K space separated integers: the indices of reachable points, in ascending order.

Constraints

• 2 ≤ N ≤ 4000
• 10 ≤ R ≤ 200
• 0 ≤ x_i, y_i ≤ 1000
• It is guaranteed that at most 200 reachable points exist.

Sample

This testcase corresponds to the animation shown above. All 28 points can be reached by the circle.