You are given a tree with N nodes and non-negative weight edges. The tree root is 1.
You need to compute the Kth smallest cost of a path from any node to any of its descendants.
If there are less than K such paths, print -1. If there are multiple paths with the same cost, they should all be counted separately.
Input
The first line of input contains two space-separated integers: N and K.
The following N - 1 lines describe the tree. Each of these lines contains three space-separated integers: x, y and w, describing an edge of weight w between nodes x and y.
Output
The output contains exactly one integer: the Kth smallest cost of path that links some node to one of its descendants.
Constraints
- 1 ≤ N ≤ 105
- 1 ≤ K ≤ N * (N - 1) / 2
- 0 ≤ weight of any edge ≤ 104
Sample
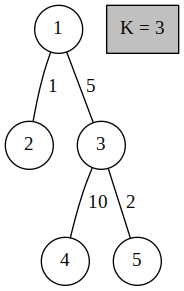
| Input | Output | Explanation |
|---|---|---|
| 5 3 1 2 1 1 3 5 3 4 10 3 5 2 | 5 | The paths from 1 to its descendants are:
If we sort all the costs we get the following sequence:
 |
Suppose we want to count how many ancestor-descendant paths have a cost of at most x (arbitrarily fixed). In order to do this, we can compute:
- ancestor[j][i] = the 2jth ancestor of vertex i (or 0 if i has less than 2j ancestors)
- cost[j][i] = the cost of the path from i to ancestor[j][i]
Having these two tables, we can climb logarithmically from any vertex to its highest ancestor such that the cost of the path between them does not exceed x. Therefore we can find the answer for a fixed x in O(N * log(N)).
Now, we need to find the lowest x such that there exist at least K paths with a cost of at most x. We can apply a binary search and solve the problem in O(N * log(N) * log(N * MAX_WEIGHT)).
Further reading: Stramosi (infoarena).
Sergiu Pușcaș - C++11
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 typedef long long ll; 5 const int nmax = 100005; 6 const int logmax = 18; 7 8 ll k; 9 int n, a, b, x; 10 int cost[logmax][nmax], ancestor[logmax][nmax]; 11 bool seen[nmax]; 12 vector <pair <int, int>> v[nmax]; 13 14 void explore(int x) { 15 seen[x] = true; 16 17 for(auto t:v[x]) 18 if(!seen[t.first]) { 19 cost[0][t.first] = t.second; 20 ancestor[0][t.first] = x; 21 explore(t.first); 22 } 23 } 24 25 int climb(int i, ll energy) { 26 if(ancestor[0][i] == 0 || cost[0][i] > energy) 27 return 0; 28 29 int j=0; 30 while(ancestor[j+1][i] != 0 && cost[j+1][i] <= energy) 31 j++; 32 33 return (1<<j) + climb(ancestor[j][i], energy - cost[j][i]); 34 } 35 36 ll how_many_paths(ll energy) { 37 ll ret = 0; 38 for(int i=2; i<=n; i++) 39 ret += climb(i, energy); 40 41 return ret; 42 } 43 44 int main() { 45 cin>>n>>k; 46 47 for(int i=1; i<n; i++) { 48 cin>>a>>b>>x; 49 50 v[a].push_back(make_pair(b, x)); 51 v[b].push_back(make_pair(a, x)); 52 } 53 54 explore(1); 55 56 for(int j=1; (1<<j)<=n; j++) 57 for(int i=1; i<=n; i++) { 58 ancestor[j][i] = ancestor[j-1][ancestor[j-1][i]]; 59 cost[j][i] = cost[j-1][i] + cost[j-1][ancestor[j-1][i]]; 60 } 61 62 ll lo = 0, hi = 1000000007LL, mid; 63 while(hi - lo > 1) { 64 mid = lo + (hi - lo) / 2; 65 66 if(how_many_paths(mid) >= k) 67 hi = mid; 68 else 69 lo = mid; 70 } 71 72 if(how_many_paths(hi) < k) 73 hi = -1; 74 75 cout<<hi<<"\n"; 76 return 0; 77 }


