Let's consider a X×Y rectangle with the middle (X-2)×(Y-2) rectangle cut out. We will call this figure a frame with size X×Y. Picture 1 shows the frame 5×6.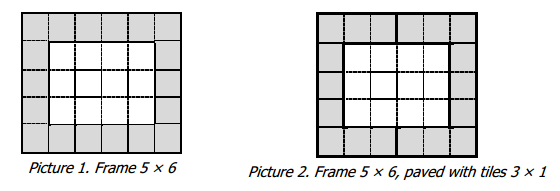
Let's assume that we have unlimited number of tiles with size A×1. We consider the following problem: is it possible to completely pave a frame with size X×Y using these tiles (tiles can be rotated by 90 degrees)? For example, frame 5×6 from Picture 1 can be paved completely with tiles of size 3×1 (one way to do so is shown in Picture 2), but can't be paved with tiles of size 4×1.
Input
The input contains several test cases, each of them as described below.
The first line contains 2 integers - X and Y.
The second line contains integer N - the number of tile types to be analyzed.
Each of the following N lines contains one integer, not exceeding 106. We designate with Ak the integer on the (k+2)th line of the input.
Output
For each test case, your goal is to print N lines, where the Kth line should contain the word 'YES', if it is possible to tile the X×Y sized frame with tiles Ak×1, and the word 'NO' otherwise.
Constraints
- 3 <= X, Y <= 106
- 1 <= N <= 1000
Sample
| Input | Output |
|---|---|
| 5 6 2 3 4 | YES NO |


