Let G = (V, E) be a weighted oriented multigraph. A vertex T ∈ V is called special if there exists at least one negative cycle that is accessible from T. Please compute the number of special vertices of G.
Input
The first line of input contains |V| and |E|.
Each of the following |E| lines contains a triple (x, y, w), denoting an edge x → y of weight w.
Output
A single integer — the number of special vertices of G.
Constraints
- 1 ≤ |V| ≤ 100 000
- 1 ≤ |E| ≤ 250 000
- 1 ≤ x, y ≤ |V|
- -104 ≤ w ≤ 104
Sample
| Input | Output | Explanation |
|---|---|---|
| 6 6 1 2 5 1 3 3 3 6 -1 5 5 -1 2 4 -2 4 2 1 | 4 | There are two negative cycles:
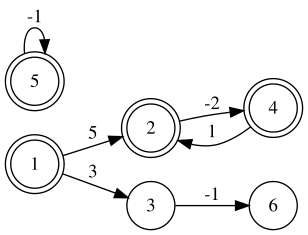 |
Solution by Gabriel-Robert Inelus
We have to make a couple important trivial notes which count towards solving the problem:
- any cycle lies entirely inside a strongly connected component;
- given a strongly connected component, we can detect whether it contains a negative cycle using the Bellman-Ford algorithm.
Hence, we can solve the problem by following the steps:
- decompose the graph into strongly connected components and build the SCC graph the same time (for example using the Kosaraju-Sharir algorithm)
- apply the Bellman-Ford shortest path algorithm on each SCC and keep track of the components which have a negative cycle
- having the DAG of the SCC's, we can run a modified topological sort using a queue. Instead of the classic algorithm (pushing into the queue all the nodes with OUT degree 0 and removing them along with any edge that is incident to them and then repeating the process while possible), we add the condition that we push into the queue only the nodes which represent a strongly connected component (nodes of SCC Graph) that have no negative cycles inside.
The worst case time complexity is:
- O(N+M) - SCC
- O(N*M) - Bellman-Ford
- O(N+M) - the modified topological sort.
Thus, the final complexity is O(N*M) due to Bellman-Ford. However, we all know that Bellman-Ford is a probabilistic algorithm; Hence, in general, it performs better than O(N * log N).
I leave as homework to the curious reader the following claims:
By using the fact that Bellman-Ford (probabilistic algorithm) usually runs faster then Dijkstra's algorithm, I claim that if there are no negative cycles in a strongly connected component of size S, each node will be pushed into the queue at most log S times. This imposes the expected O(S * log S) time complexity.
We can pick a constant c, such that log |maxS| < c = 60 and claim with a very high success rate that if a node is pushed into the queue for more than 60 times, then it is a member of a negative cycle. Even though this runs fast (less than half a second per testcase on an average computer for 105 vertices and 2.5 * 105 edges), this solution is non-deterministic and may fail on a smart particular test. The success rate increases as the constant gets larger and hits certainty when c = S, considering that a node that is pushed into the queue S times must be a member of a negative cycle.


