Our friends at Bitdefender want to develop a newer, better, faster, stronger antivirus program. They realized that the software works best if all 2*N computers in the network are arranged in a circle, and each computer is tied to exactly one other peer with a straight cable. Each pair of computers tied together is associated a unique ID, for the sake of simplicity.
This layout is encoded as 2*N integers: the IDs of each computer you encounter if you start at some point on the circle and traverse it in clockwise order once. Naturally, each value between 1 and N will occur twice (once for each endpoint of a connected pair of computers).
Due to the physical arrangement of the computers, the engineers noticed that some of the cables intersect each other. Now they are wondering whether or not it is possible to compute how many pairs of intersecting cables there are, based on a given layout.
Input
The first line of input contains N - the number of cables.
The second line of input contains 2*N integers - the network layout.
Output
A single integer: the number of overlapping pairs of cables.
Constraints
- 1 ≤ N ≤ 50 000
Sample
| Input | Output | Explanation |
|---|---|---|
| 3 1 2 3 2 3 1 | 1 | The only segments that intersect are 2 and 3.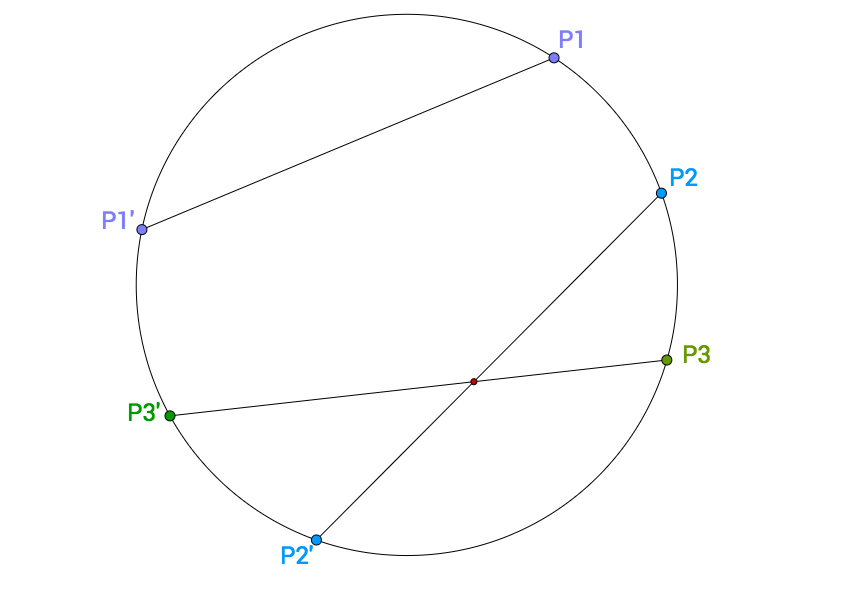 |
Let's denote:
- first[x] = the position of the first occurence of x
- second[x] = the position of the second occurence of x
In other words if we consider for each cable the interval [first[i], second[i]], then, we must count the number of pairs that intersect each other, but are not fully contained one in the other.
We can take advantage of the fact that these intervals are already sorted by their beginning.
We will proces each number from the input. Suppose we are at number i. If this is the first i we've encountered, then we will insert it in data structure. If it is the second one, then we need to query the data structure to get how many intervals are opened in the interval first[i], second[i], but close after second[i]. Because we process each point in sorted order, we can keep a segment tree or a similar DS that can provide add(pos, value) and getSum(x, y)


