100 - MaxRev
200 - Balls
Let's examine the case with 9 balls.
First of all, we can group the 9 balls in the 3 groups, each having 3 balls. Let's call them group1, group2 and group3.
We will weight 2 of them and it will result some cases:
- (group1 == group2) - if the 2 groups we weight are equal then the heavier ball will be in the 3rd group which we have not weighted yet (group3)
- (group1 != group2) - if one of them is heavier then we have found the group which is heavier so either group1 or group2
Now we only have 3 balls left to weight (in each of the 2 cases described above). We apply the same idea again. So, we will weight only 2 balls and see if they are equal then the heavier is the 3rd one. Else one of the 2 balls is the one.
So we have managed to find the heavier ball by making only 2 weighings. Now we can apply the same idea (of splitting the input into 3 groups) to any input. So, the answer will be log3(n-1) which can be calculated in O(1) or in O(log3(n))
250 - SpeedV2
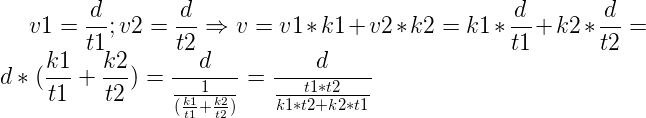
350 - Morse
For every word we will do the following:
Let's say we are at word W(i). We compute its morse encoding and using a mapping from morseEncoding to number of apparitions, we will keep track of how many times a morse encoding appeared in the dictionary.
So at step i we will increment the number of apparitions of the morse encoding we obtained from W(i) where i=1...n. In order the manage this mapping we can use a hash table that maps strings to integers. We can then compute the answer by iterating through the values of the hash.
If there are no collisions, we print -1.
Let's say we are at word W(i). We compute its morse encoding and using a mapping from morseEncoding to number of apparitions, we will keep track of how many times a morse encoding appeared in the dictionary.
So at step i we will increment the number of apparitions of the morse encoding we obtained from W(i) where i=1...n. In order the manage this mapping we can use a hash table that maps strings to integers. We can then compute the answer by iterating through the values of the hash.
If there are no collisions, we print -1.
#include <iostream> #include <stdio.h> #include <unordered_map> #include <vector> using namespace std; int main() { int n, ans = 0; vector <string> d; unordered_map<char, string> repr; unordered_map<string, int> cnt; for(int i = 0; i < 26; ++ i) { char ch; string code; cin >> ch >> code; repr[ch] = code; } cin >> n; for(int i = 0; i < n; ++ i) { string word; cin >> word; string morse = ""; for(auto ch : word) morse = morse + repr[ch]; ans = max(ans, ++ cnt[morse]); } if(ans == 1) cout << -1 << '\n'; else cout << ans << '\n'; return 0; }


